How Common Core Dictates Teaching Style
I believe that CC math, while not dictating particular teaching styles, has thrown gasoline on the ideological fire that has been raging for slightly more than two decades in education. I am referring to what is known as “reform math.” Reform math has manifested itself in classrooms across the United States mostly in lower grades, in the form of “discovery-oriented” and “student-centered” classes, in which the teacher becomes a facilitator or “guide on the side” rather than the “sage on the stage” and students work so-called “real world” or “authentic problems.” It also has taken the form of de-emphasizing practices and drills, requiring oral or written “explanations” from students on how they solved a problem (besides showing their work), finding more than one way to do a problem, and using cumbersome strategies for basic arithmetic functions. Math reformers say such practices will result in students understanding how numbers work—i.e., math is about “understanding,” not simply “doing”.
CC lends itself to such interpretations because of the words “explain” and “understand” in their content standards as well as eight overarching standards called “Standards for Mathematical Practice” that embody “habits of mind” of mathematical thinking. On the surface and to those unaware of underlying concerns and issues, the SMPs appear reasonable. But they are being interpreted to force students into developing “habits of mind” outside of the context of the material being learned—which again feeds into the reform math ideology.
CC’s own documentation of the standards discusses understanding as a major shift in how math should be taught:
The standards call for conceptual understanding of key concepts, such as place value and ratios. Students must be able to access concepts from a number of perspectives in order to see math as more than a set of mnemonics or discrete procedures.
I agree with Green that teachers need more pedagogical training, but not the type she envisions. I would like to see schools of education focus on what has proven to have worked in the past. The traditional approaches that Green believes are responsible for math education “not working” actually encompass many techniques she likes. These would include inductive learning, trial-and-error learning, teach-by-groups, and even guided discovery.
MORE NEWS: Know These Before Moving From Cyprus To The UK
Implementation Is Not the Problem
In Green’s view, reform math is how math should be taught because math is about “understanding”. And since CC emphasizes “understanding” rather than just doing, it is the way to teach math and do Common Core. In the world according to Green, if math is taught poorly it is either because 1) it is taught in the traditional manner or 2) it was reform math executed poorly. This leaves a nice out for both types of teaching. Pointing to reform math as a possible reason for the bad performance of students over the last two decades is responded to by saying “It wasn’t true reform math.”
But reform math in the United States is done poorly, according to Green, which provides her a handy out to the many examples of ridiculous problems and incomprehensible homework assignments attributed to CC. She agrees, they are bad and not what CC is about. Green writes “With the Common Core, teachers are once more being asked to unlearn an old approach and learn an entirely new one, essentially on their own. Training is still weak and infrequent, and principals—who are no more skilled at math than their teachers—remain unprepared to offer support.” She holds in disdain the “I, we, you” model of classroom teaching (and which is one of the few techniques actually supported by research) and argues instead for “You, Y’all, We”/discovery learning. And to bring that off requires teacher training that is “meaningful”—i.e., allowing for properly implemented reform ideas and Common Core.
Green argues that reform math done right does work, pointing to Japan for evidence. She claims Japan is doing U.S.-style reform correctly. Japan’s method of teaching is admittedly different in how teachers collaborate to create “lesson plans” and anticipation of student misunderstandings and questions. But Green fails to acknowledge that Japanese instruction is strongly teacher-led and does not rely on discovery. A paper by Alan Siegel, a math professor at New York University, provides valuable insight into myths about Japanese teaching and shows that it is based on whole class and direct instruction techniques—and much practice.
Green recommends more training in order to make reform math work. She also laments that many teachers lack knowledge of the math they are teaching. This may be more prevalent in lower grades than middle and high school, for which the credentialing procedures require passing more comprehensive math proficiency exams. But well-organized math textbooks that contain explanations and worked examples would go a long way toward fixing the problems of both students and teachers. Furthermore, there are plenty of math-literate parents who have a hard time understanding the point of the reform-oriented math exercises, so teachers are not the only ones struggling.
How to Do Common Core Math Well
This brings me to the next part of my article. I have selected some standards from the first- and second-grade CC math and have provided descriptions of what I believe are sensible interpretations and implementations of them. In addition, I describe ineffective and destructive ways that they are being interpreted—some of which have been documented in articles and on television.
I will be doing more of these in the future to provide alternatives to guidance that schools and teachers are being handed by their districts and what appear in various textbooks that are supposedly “Common Core” aligned. If, in the meantime, Green wants to think that what I describe here is really reform math, far be it from me to tell her otherwise.
Selected First Grade Standards: Represent and Solve Problems Involving Addition and Subtraction
Standard 1.OA.A.1: Use addition and subtraction within 20 to solve word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem.
This standard calls for students to learn basic forms of addition and subtraction word problems. These include “I have 5 applies and get 2 more; how many do I have?” (Putting together), “Five apples are on the table. Three are red and the rest are green. How many apples are green?” (Taking apart). By requiring equations with a symbol for the unknown number to represent the problem (although pictures or diagrams can be used in lieu of algebraic symbols) students learn to apply the concepts of number bonds (e.g. 5 + 2 = 7, 7 -2 = 5, and 7 -5 = 2) to solve word problems.
Various elementary school textbooks take the approach outlined in the standards. One textbook is Singapore’s Primary Math series. Students see pictures of 7 objects broken into groups of 2 and 5, and then 4 and 3, and so on. Students learn that pairs for a particular number make up a “number family” (or “number bonds”) and they can then be taught that 5 + 2 = 7 is part of a family in which 7 – 2 = 5 and 7 – 5 = 2. Students can then express an equation such as 5 + n = 7 as 7 – 5 = n, and then give the answer to what is a now-familiar math fact. They can then apply this principle to solve basic word problems, such as “John has some apples. He gets two more and now has a total of 5. How many did he have to start with?”
The ability for first graders to represent word problems with equations and to solve such equations with a symbol for unknown number (in all positions) will vary. The belief informing this particular standard is likely the ever-popular myth that learning number facts by memorization only is “rote” and doesn’t lead to “deep understanding” as do the strategies for doing addition. The part-whole relationships that form the conceptual underpinning of this standard are abstract for some first graders, however.
MORE NEWS: How to prepare for face-to-face classes
While Singapore’s Primary Math series expect familiarity with numbers and development of mental tricks (for ease of computation), the expectation is one in which such development will evolve naturally. The Singapore textbooks do not insist on the specific methods that are embedded in Common Core’s standards. Thus, teachers should differentiate instructions so students who have difficulty with using a letter for a number are given alternatives, and can rely on pictorial representations.
Of particular note is that parents have complained that their first grade children have been asked to explain why two numbers sum to another (e.g., why is 2 +3 equal to 5?) Such requirement is inappropriate. Not only are such exercises misguided and erroneous, but they do not contribute to any kind of “deeper understanding” of mathematics. Furthermore, it is extremely questionable whether any kind of deeper understanding of addition and subtraction is necessary for first graders. Breaking apart numbers will occur again in other grades in other contexts, so that the initial understanding of addition is built upon. I question how many of those pushing for “deep understanding” actually learned that way in first grade.
The use of number bonds to solve elementary addition and subtraction equations is not limited only to Singapore’s math textbooks. It has also been used extensively in U.S. textbooks, such as a third grade textbook popular in the 1950’s (Brownell, et. Al., 1955), as shown below. I include this example because it shows that: 1) such procedures were used in classrooms during an era decried for teaching math using “rote memorization” without understanding, and 2) such technique may be repeated and more appropriate in later grades.
Standard 1.OA.C.6: Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decomposing a number leading to a ten (e.g., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); using the relationship between addition and subtraction (e.g., knowing that 8 + 4 = 12, one knows 12 – 8 = 4); and creating equivalent but easier or known sums (e.g., adding 6 + 7 by creating the known equivalent 6 + 6 + 1 = 12 + 1 = 13).
This appears to be straightforward and for the most part it is. In fact the standard itself is contained in the first sentence: “Add and subtract within 20, demonstrating fluency for addition and subtraction within 10.” The remainder of the standard, for all practical purposes, dictates pedagogy (i.e., “use strategies”), and then suggests specific types of strategies to use.
Apologists for the Common Core standards will point out that the standards are not telling what the teachers should do but what students should be able to do. If the goal of the standards is for students to have a toolkit of strategies to use, then the strategies contained in the above standard should be read as suggestions for teachers to consider among other alternatives.
The strategy of “counting on”, for example, is commonly used in teaching addition and is appropriate for first graders. The strategy of “making tens” may be difficult for some first graders, however, as may be using equivalent sums. While the process of “making tens” is used in Singapore’s “Primary Math” first grade textbook, it is one of several strategies presented that students may choose to use. There is no requirement that I’ve observed in Singapore’s textbooks that forces first graders to find friendly numbers like 10 or 20. This is probably because many first graders likely come to learn that 8 + 6 equals 14 through memorization, without having to repeatedly compose and decompose numbers in order to achieve the “deep understanding” of addition and subtraction that standards-writers feel is necessary for six-year-olds.
Insisting on calculations based on the “making tens” and other approaches are in my opinion not likely to prove useful for all first graders. Teachers should be free to differentiate instructionso that those students who are able to use these strategies can achieve those goals. It is unrealistic and potentially destructive to interpret the Common Core math standards as requiring that all first grade students use these strategies.
“Making tens” is not limited to Singapore’s math textbooks, nor is it a new strategy. It has been used for years, as shown from a third-grade arithmetic textbook (Brownell, et al, 1955).
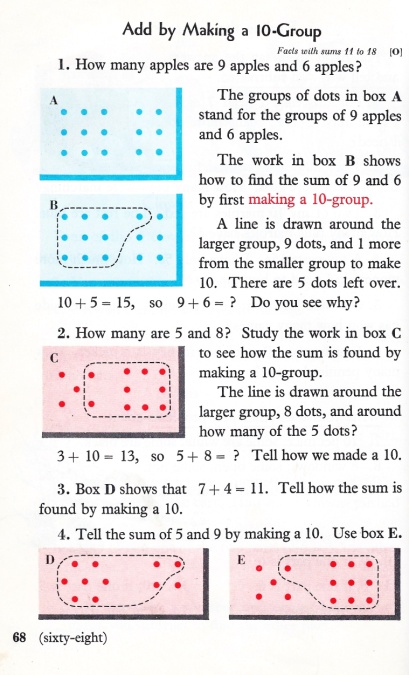
Some students may be able to “make tens” through dot pictures as shown above; others may be able to make tens in their heads—which is the ultimate goal—without the intermediate aid of the pictures.
Selected Second Grade Standards: Use Place Value Understanding and Properties of Operations to Add and Subtract
We move now to second grade and, in particular, to multi-digit addition and subtraction and the following standards:
CCSS.Math.Content.2.NBT.B.5 Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
CCSS.Math.Content.2.NBT.B.6 Add up to four two-digit numbers using strategies based on place value and properties of operations.
CCSS.Math.Content.2.NBT.B.7 Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.
CCSS.Math.Content.2.NBT.B.9 Explain why addition and subtraction strategies work, using place value and the properties of operations.
The Common Core grade-level standards are minimum levels of expectation and goals, and are to be met no later than that particular grade level. Thus, the standards do not prohibit teaching a particular standard earlier than the grade level in which it appears. The standard algorithm—which is the classic and most efficient procedure—for multi-digit addition and subtraction is developmentally appropriate for second graders. The algorithm appears in the fourth grade standards (4.NBT.B.4) and states: “Fluently add and subtract multi-digit whole numbers using the standard algorithm.” It should be the prevailing method for adding and subtracting numbers, starting in second grade. At a minimum, the standard algorithm should be taught using three-digit numbers.
Delaying teaching of the standard algorithm until fourth grade and relying on place value “strategies” and drawings to add numbers is thought to provide students with the conceptual understanding of adding and subtracting multi-digit numbers. What happens, instead, is that the means to help learn, explain or memorize the procedure become a procedure unto itself and students are required to use inefficient cumbersome methods for two years. This is done in the belief that the alternative approaches confer understanding, so are superior to the standard algorithm. To teach the standard algorithm first would in reformers’ minds be rote learning. Reformers believe that by having students using strategies in lieu of the standard algorithm, students are still learning “skills” (albeit inefficient and confusing ones), and these skills support understanding of the standard algorithm. Students are left with a panoply of methods (praised as a good thing because students should have more than one way to solve problems), that confuse more than enlighten.
The methods are side dishes that ultimately become indistinguishable from the main dish of the standard algorithm. As a result, students can become confused—often profoundly so. As Robert Craigen, math professor at University of Manitoba describes it: “This out-loud articulation of ‘meaning’ in every stage is the arithmetic equivalent of forcing a reader to keep a finger on the page, sounding out every word, every time, with no progression of reading skill.”
Teaching the standard algorithm in the second grade, however, allows the other strategies to be used to highlight how the standard algorithm works, thus effectively complementing its procedure. Note that Standard NBT.B.7 calls for students to “understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.” The word “understand” is used in many of the content standards. Common Core standards have been interpreted so that students are expected to provide an explanation of what is happening mathematically, which is largely impossible for many students in lower grades. Instead, a more realistic interpretation of this word is that students show a procedural understanding of addition and subtraction as described in the standard itself; i.e. combining numbers of the same place value.
In that vein, standard 2.NBT.B.9 calls for students to explain how addition and subtraction strategies work in terms of place value. This particular standard has a footnote that says that pictures and diagrams can be used. The approach taken in Arithmetic We Need, Grade 3 (Brownell et al, 1955) provides an example of the form an explanation can take:

In the text above, the student is given explicit instruction on what they are to demonstrate and then asked to solve four problems in the three ways shown in the diagram. It is important to note that this is the only time in the textbook the student is asked to do this particular strategy. Doing such methods for a few problems (four or five) is sufficient for students to see how the place value and properties of addition and subtraction work. Asking students to do this routinely for many problems is unnecessary—and certainly not for a two year period. Strategies can get out of hand and make simple problems unnecessarily difficult, and cause profound confusion rather than instilling “understanding. This video illustrates this phenomenon.
More Common Core Reinterpretations Ahead
Here, I have provided examples of how it is possible to interpret the Common Core math standards in a sensible manner that does not fall back on questionable and ineffective education practices. One has to accept that procedural fluency is essential for students to achieve and that ultimately it leads to understanding. One also has to realize that not all students will achieve the same level of understanding at the same time; sometimes understanding of a procedure or problem solving approach comes later. I will address other standards in subsequent articles, and would very much value readers’ interpretations of and approaches for teaching other CC math standards. (That includes teachers.) In so doing, I would also welcome seeing effective and time-tested approaches to teaching methods, as well as procedures and concepts described in other textbooks from various eras. Needless to say—but I’ll say it—this invitation is extended to Elizabeth Green.
Reference
Brownell, Guy T., William A. Brownell, Irene Saubel. “Arithmetic We Need; Grade 3”; Ginn and Company. 1955.
Image by Oakley Originals.


Join the Discussion
Comments are currently closed.